[첨단 헬로티]

초스마트 사회 실현을 위해서는 대규모 도시 시스템의 이종·이구조 계층적 사이버 피지컬 시스템(Cyber Phy-sical System : CPS)으로서 모델링과 제어·최적화가 중요하다는 것은 말할 필요도 없지만, 이에 더해 에너지 관리, 인프라 제어, 주민의 의사결정과 반영법을 모두 다룰 필요가 있다.

지금까지는 각각의 사회 인프라 시스템이 독립적으로 관리·제어되어 왔기 때문에 수직적인 시스템의 최적화만 이루어지고, 사회 전체의 효용이나 주민의 이익이 충분히 고려되지 않았다. 지구적 관점에서 온난화·에너지 문제를 해결하면서 대규모로 복잡화되는 도시 기능을 건전하게 발전시키기 위해서는 이종·이구조의 사회 인프라 시스템을 수평방향으로 연결시켜 구조적으로 다루는 시스템을 만드는 것이 중요하다.

전력 네트워크는 도시 인프라의 근간을 이루는 대규모 복잡 계층형 시스템이라고 할 수 있다. 에너지 문제나 지구 온난화가 세계적으로 긴급한 과제가 되고 있으며, 에너지 절감, 코스트 절감의 관점에서 세계적으로 태양광 발전이나 풍력 발전 등의 분산형 전원이 대량으로 전력계통에 연계되고 있다. 그러나 동시에 분산 전원을 대량으로 도입한 전력 네트워크에서는 주파수 변동이나 전압 변동이 발생할 위험성을 가지고 있기 때문에 안전성을 확보한 후에 각 발전기를 협조시키면서 최적의 발전을 할 필요가 생긴다. 일본에서는 전력 자유도가 계획적으로 진행되고 있으며, 보다 고도의 분산형 제어 기술의 구축을 기대하고 있다.

또한, 기능적인 교통 네트워크를 형성하는 것은, 말할 필요도 없이 도시 인프라 시스템 관리를 위해 매우 중요하다. 교통량 증가에 따른 정체는 사회 문제가 되어 있으며, 일본 국내에서도 정체에 의해 전국 각지에서 사회적으로 큰 손실이 발생하고 있다. 이러한 도로 교통 정체 문제에 대해, 고도 도로 교통 시스템(Intelligent Transport Systems : ITS)에 기초하는 여러 가지 정체 해소 방법이 제안되고 있다. 그러나 현재 개발이 기대되는 자동 운전 기술의 도입과 유효한 이용을 위해서는 아직 더 고도의 기술 개발이 필요하다.

도시 인프라의 전력 네트워크나 교통 네트워크 제어 시에는 인간의 의사결정에 자연스러운 형태로 개재하는 스마트 시스템 설계가 필수이며, 인간의 의사결정에 관여하기 위해서는 게임 이론에 근거한 경제적인 메커니즘 설계가 합리적인 접근일 것이다. 전력 시스템에서는 수요가의 전력 소비량 평준화에 대한 동적인 전력 가격 결정의 유효성이 지적되고 있으며, 교통 시스템에 관해서는 미국과 유럽 국가들에서 볼 수 있는 HOV(High Occupancy Vehicle) 레인(다인승 차량 전용 차선)의 도로이용료 가변 가격 제도가 정체 해소에 큰 효과를 거두고 있다. 그러나 이러한 가상 환경이나 적용 가능 범위는 이론적으로도 매우 제한적이며, 응용 전개의 관점에서도 유효성이 아직 충분히 검증되지 않았다.

현재 전력, 교통, 경제, 인간 행동이 변동하는 환경 하에서 여러 가지 요인에 의해 복잡하게 연계된 사회 인프라 시스템에 대해, 시스템 제어에 의한 통합 관리 메커니즘의 구축이 기대되고 있다. 이 글에서는 도시의 계층 구조를 에너지와 교통 시스템의 관점에서 통합한 정보·에너지·교통의 지역 통합 관리 시스템의 기본적인 개념과 에너지·교통 통합 관리 시스템의 예로서, 게임 이론에 기초한 시스템 제어 접근을 이용한 고속도로의 전기자동차 비협력 최적 충전 스케줄링 문제를 소개한다.

에너지·교통 통합 관리 시스템

지역의 정보·에너지·교통의 결합 예를 그림 1에 나타냈다. 지역의 중심에는 대형 쇼핑센터가 있고, 맨션, 단독주택, 재생 가능 에너지 발전시설, 또한 신전력, 전력회사 등의 플레이어(의사결정 주체)가 여러 개 존재하며, 지역에는 비영리조직인 CEMS(Community Energy Mana-gement System)가 에너지 관리·감시를 하고 있는 상황을 가정한다.

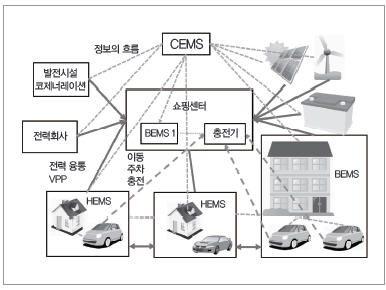
▲ 그림 1 지역의 정보·에너지·교통의 통합 관리

단독주택에는 HEMS(Home Energy Management System)가 설치되어 있으며, 그 중 일부는 전기자동차를 소유하고 있다. 또한, 맨션이나 빌딩에는 BEMS(Building Energy Management System)가 배치되어 있다. 여기에서 굵은 실선은 에너지의 왕래를 나타내고, 쇄선은 교통 흐름을 나타내며, 점선은 정보의 결합을 나타낸다. HEMS-HEMS 사이에서 Peer to Peer(P2P)의 전력 에너지 융통이나 전기자동차의 배터리를 이용한 Virtual Power Plant(VPP) 서비스가 블록체인 기술에 기초해 가동된다. 각 가정에서는 쇼핑센터에 쇼핑하러 가고, 또한 거기에서는 급속 충전기를 이용할 수 있다.

주차장 요금은 변동형으로 되어 있으며, 집객이나 혼잡 해소에 이용할 수 있다. 또한, 대형 주차장에는 스마트 파킹 시스템이 도입되어 있어, 이용자는 앱을 통해 수수료를 지불하고 주차 슬롯을 사전에 예약할 수 있다. CEMS는 지역 전체의 에너지 균형과 교통량, CO2 배출량을 감시하고, 플레이어에게 정보를 제공함으로써 간접적으로 지역을 관리한다.

스마트 시티의 설계 문제란 그 규칙의 책정과 사회 전체의 후생 함수 최대화와 개인(플레이어)의 효용 함수 최대화의 방향성을 최대한 일치시키는 문제라고 할 수 있을 것이다.

이하에서는 에너지·교통 통합 관리 시스템의 예로서, 더 구체적인 고속도로의 전기자동차 비협력 최적 충전 스케줄링 문제에 대해 소개한다. 이때에 사람의 의사결정을 처리할 필요가 있기 때문에 여기에서는 게임 이론에 기초하는 시스템 제어 접근을 이용한다.

전기자동차 비협력 최적 충전 스케줄링

전기자동차(EV : Electric Vehicle)는 가솔린자동차나 디젤자동차와 비교해 한번 충전으로 주행할 수 있는 거리가 상당히 짧기 때문에 고속도로 주행으로 대표되는 장거리 주행 시에는 충전을 할 장소와 시간을 미리 계획하는 것이 필요하다. 이 계획 문제를 전기자동차 충전 스케줄링 문제라고 부른다.

미국에서는 전기자동차의 보급에 따라 Car Charging 등의 사업자가 충전 스테이션을 제공하고 있다. 그 외에도 중국의 일부 지역에서는 EV 소유자는 전기요금 이외의 추가 요금을 지불하고 EV를 충전할 필요가 있으며, 그 가격은 사업자가 자유롭게 결정할 수 있다. 이와 같이 충전 스테이션 수가 증가함에 따라 각 스테이션 간의 가격 경쟁은 심화될 것으로 생각되며, 스테이션 관리자는 자신의 이익을 최대화할 수 있는 가격 설정 방법을 찾아낼 필요가 있다. 가령 하나의 충전 스테이션에 많은 EV가 집중된 경우, 스테이션 관리자는 이익을 손해보게 되기 때문에 모든 충전 스테이션 이용률이 일률적으로 되는 것이 바람직하다.

한편, EV의 소유자는 자신의 목적에 따라 충전 스테이션을 선택한다. EV 소유자들이 서로 협력하여 스케줄링을 달성하는 협조 알고리즘은 이미 제안되고 있다. 하지만 EV 소유자들이 서로 협력하는 상황이 반드시 현실적이지는 않으며, EV끼리 이기적인 거동을 보여 서로 경쟁하는 상황을 생각하는 것도 필요할 것이다. 이 장에서는 이러한 비협력 충전 스케줄링 문제에 대해, EV와 충전 스테이션을 각각 플레이어로 간주한 계층형·반복·비협력 게임으로 분류되는 슈타켈베르크(Stackelberg) 게임을 이용함으로써 EV끼리의 경쟁 메커니즘이나 충전 스테이션과 EV 간의 행동 결정 순서를 표현할 수 있다.

이 연구에 이용되는 스케줄링 문제의 개요를 그림 2에 나타냈다. 각 충전 스테이션은 동일한 관리자에 속하는 것으로 하고, 충전 스테이션 간의 통신(I2I)를 이용해 상호의 정보를 교환한다. 각 스테이션은 스케줄링 시간 k=nT(n=1, 2, ...)에 충전 가격을 각 차량에 제시하고, 각 EV는 가격을 바탕으로 원하는 충전 수요량을 충전 스테이션에 제시한다.

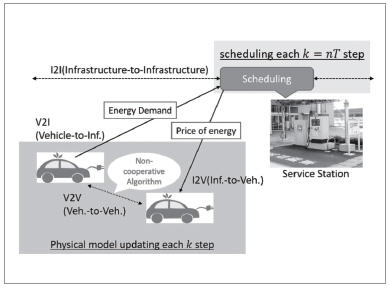
▲ 그림 2 충전 스테이션 스케줄링 문제

1. 교통 흐름 모델

그림 3과 같은 한방향 고속도로와 그 교통 흐름을 생각한다. 고속도로 출입구 혹은 충전 스테이션이 존재하는 서비스 지역을 하나의 노드로 하고, 모든 노드 수를 N으로 한다. 한 노드 i에 도착하는 모든 EV 수 αi(k)는

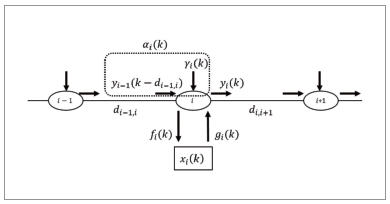
▲ 그림 3 교통 흐름 모델

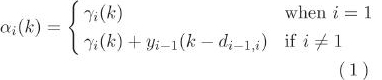
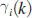는 노드 i에 있어 모델 외부에서 유입해 오는 EV 수, yi-1(k)는 노드 i-1를 시간 k에서 출발한 EV 수, di-1,i는 노드 i-1에서 노드 i까지의 소요 시간이다. 또한, yi(k)는

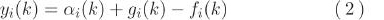
여기에서 fi(k)는 충전 스테이션 i에 유입해 오는 EV 수, gi(k)는 충전 스테이션 i에서 유출하는 EV 수이다.

2. 충전 스테이션 모델

이 모델을 이용해 충전 스테이션 내의 차량 거동을 표현한다. 충전 스테이션 i에 존재하는 EV 수를 xi(k)≥0으로 둔다. 그림 3에서 이하의 식을 얻을 수 있다.

3. EV 충전 모델

EV의 SOC(State of Charge) 추이는 이하의 식과 같이 표현된다.

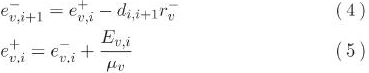
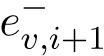은 어떤 EVν이 노드 i+1에 도착했을 때의 SOC, 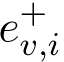는 EVν이 노드 i를 나왔을 때의 SOC를 나타낸다. 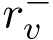는 단위 시간의 주행에 필요한 SOC이다. Ev, i는 EVν가 노드 i에서 충전하는 에너지량,μν>는 배터리 용량이다. 충전에서 각 EV는 이하의 2가지 제약 조건을 충족시키는 것으로 한다.

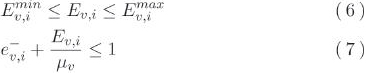
(6) 식은 EV가 충전 스테이션에서 충전할 수 있는 에너지량의 상하한 제약, (7) 식은 SOC에 관한 제약이다.

4. 슈타켈베르크 게임

시간 k에서 ci대의 충전기를 가진 SSi로 향하고 있는 EV가 Ki(k) := {1, . . . K(k)}대 존재하는 게임을 생각한다. 충전 스테이션 관리자는 EV가 에너지 수요를 달성할 수 있도록 가격조 p(k) =[p1(k), . . ., pK(k)(k)]를 제시한다. 여기에서 pν(k)는 한 EVν에 대한 전력 가격이다.

대상이 되는 EV의 충전 에너지 수요조를 E(k)=[E1,i(k), . . ., EK(k),i(k)]로 한다. 여기에서 Eν,i(k)는 어떤 EVν가 SSi에서 충전 에너지 수요량이며, EV가 충전되지 않은 경우에는 Eν,i(k)=0이 된다.

이 문제에서 EV가 원하는 에너지량을 충전 스테이션 관리자에게 전하면, 충전 스테이션 관리자는 자신의 이익을 최대화할 수 있는 충전 가격을 EV에 제시하고, EV는 제시된 가격과 다른 EV의 거동에 기초해 다시 자신의 효용을 극대화하는 에너지량을 신고하는 일련의 흐름을 반복한다. 따라서 이 문제는 계층 구조를 가진 반복·비협력 게임으로, 충전 스테이션 관리자는 EV에 대해 의사결정의 특권을 가지고 있다. 이러한 문제는 슈타켈베르크 게임의 1리더·복수 팔로워 게임 문제라고 불린다.

5. 시뮬레이션 검증

시뮬레이션 조건을 표 1에 나타냈다. 시뮬레이션 프로그램 대상을 토메이 고속도로의 도쿄-나카이 서비스 지역 간의 9노드분으로 했다. 그림 4는 시뮬레이션 대상을 노드화한 모델이다. 동그라미가 인터체인지, 네모가 충전 스폿을 가지는 서비스 지역, 인터체인지와 서비스 지역 사이의 숫자는 이동 소요 시간, 서비스 지역 아래의 굵은 서체의 숫자는 스테이션에 존재하는 EV 충전기 수를 나타낸다. 또한, 슈타켈베르크 게임의 이터레이션 횟수는 300[step]으로 했다. 외부에서 모델 내부로 유입되는 차량 수 , 각 EV의 배터리 용량과 초기 충전량은 적당히 부여했다.

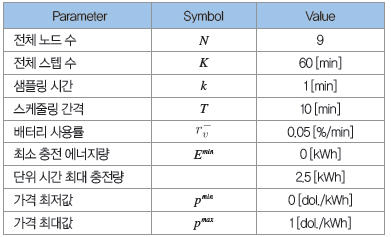
▲ 표 1 시뮬레이션용 파라미터

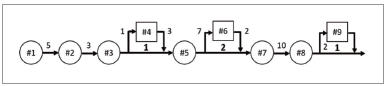
▲ 그림 4 토메이 고속도로의 노드화 모델

시뮬레이션 결과를 그림 5~그림 7에 나타냈다. 그림 5에서는 이용률이 기존의 알고리즘에 비해 향상되어 있지만, 완전히는 일률적으로 되어 있지 않다. 이것은 서비스 스테이션 SS9에서는 아직 차량이 도착하지 않으므로 당연히 차량을 유입시킬 수 없고, 이용률은 step 10-20 사이에서 0이 되기 때문이다. 그러나 그림 6, 그림 7로부터 슈타켈베르크 게임에 의한 최적 에너지 수요량과 가격이 모두 제약 내에 들어가 있는 것을 확인할 수 있다. 또한, 그림 6에서는 모든 EV에서 제약이 지켜지고 있는 것을 확인할 수 있다. 그림 7에서도 최종적인 가격은 상하한 제약 내에 들어가 있다.

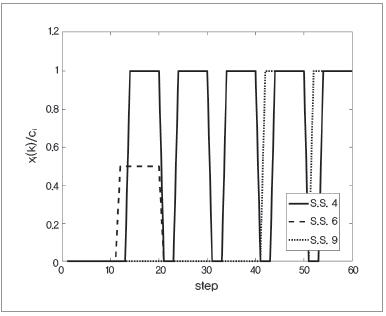
▲ 그림 5 각 SS의 이용률

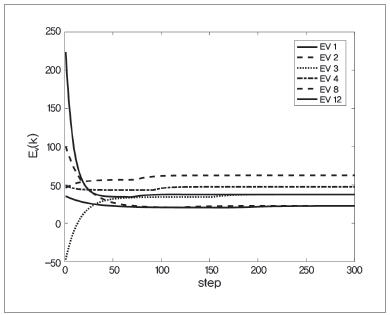
▲ 그림 6 각 EV의 충전 에너지 수요량 (k=51, node=9)

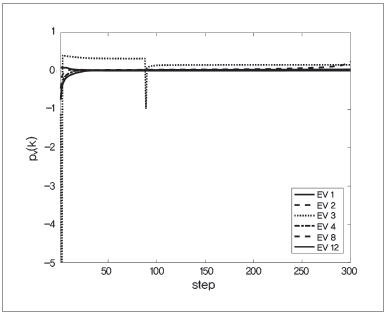
▲ 그림 7 각 EV에 대한 제시 가격 (k=51, node=9)

맺음말

이 글에서는 시스템 제어에 의한 초스마트 사회에 대한 접근으로서 에너지·교통 통합 관리의 제어 문제와 구체적인 전기자동차의 비협력 최적 충전 스케줄링 문제를 소개했다. EV 최적 충전 스케줄링 문제에서는 EV의 흐름, 충전 스테이션 내의 차량 수 추이, EV의 충전량 추이에 대해 모델화한 후, EV를 팔로워, 충전 스테이션을 리더로 한 원 리더 멀티 팔로워형 슈타켈베르크 게임 문제를 정식화했다. 또한, 마지막으로 수치 시뮬레이션을 이용해 비협력 최적 충전 스케줄링 문제와 그것에 대한 해법의 일례를 소개했다.

도시 인프라 시스템은 그 상태가 시시각각 변화하고, 정보·에너지의 결합 형태도 항상 변화한다. 이러한 결합과 분리에 대해 플렉시블한 대규모 도시 인프라 시스템을 대상으로 해, 지금까지 구축해온 분산 협조 제어 이론에 대해 ‘계층적 이구조 시스템의 Plug & Play 제어(결합·분리해도 기능이 유지되는 성질)’로 승화·전개시키는 것이 중요하다고 생각된다. 

滑川 徹

케이오대학 이공학부 시스템디자인공학과

本 記事는 日本 「計測自動制御學會」가 發行하는 「計測と制御」誌와의 著作權協定에 依據하여 提供받은 資料입니다.